Đường cao là gì? Tính chất, công thức tính một số đường cao?

Đường cao là gì? Tính chất, công thức tính một số đường cao?

Trong hình học phẳng, đường cao là một đường thẳng rất quan trọng và có rất nhiều dạng toán liên quan đến đường này. Đường cao trong tam giác là gì? Tính chất, công thức tính một số đường cao? Hãy cùng Công Decor tìm hiểu qua bài viết dưới đây nhé!

>
Đường cao trong tam giác

Đường cao là gì?

• Đường cao của tam giác là đoạn thẳng kẻ từ đỉnh đến đường thẳng chứa cạnh đối diện của đỉnh đó.
• Giao điểm giữa đường cao và đáy tương ứng được gọi là chân đường cao
• Trong một tam giác có 3 đường cao và 3 đường cao cắt nhau tại một điểm. Điểm đó được gọi là trực tâm.

Tính chất của đường cao

 Tính chất của đường cao trong tam giác cân

• Trong tam giác cân, đường cao tương ứng với cạnh đáy là vừa là đường trung tuyến vừa là đường phân giác.
• Nếu tam giác bất kỳ có đường cao đồng thời là đường trung tuyến hoặc đường phân giác thì tam giác đó là tam giác cân.
• Đặc biệt: Tam giác đều là trường hợp đặc biệt của tam giác cân. Do vậy, đường cao trong tam giác đều có tính chất tương tự như tam giác cân

Tính chất của đường cao trong tam giác vuông

• Đường cao trong tam giác vuông là cạnh góc vuông và đáy là cạnh góc vuông còn lại.

Tính chất của đường cao trong tam giác vuông cân

• Tam giác vuông vừa là tam giác vuông vừa là tam giác cân.
• Đường cao trong tam giác vuông cân là đường trung tuyến, vừa là đường phân giác của tam giác đó.
• Độ dài của đường cao kẻ từ đỉnh góc vuông bằng ½ cạnh huyền.

Công thức tính một số đường cao

Công thức tính đường cao trong tam giác thường

Áp dụng công thức Hero:

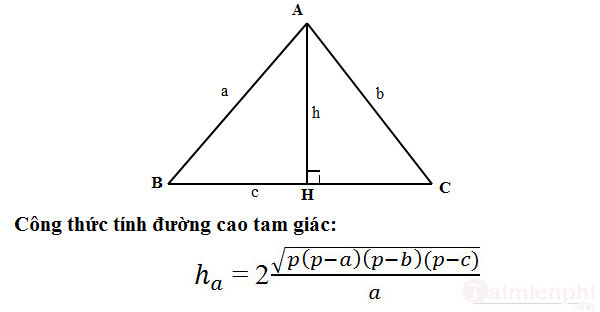
Trong đó: ha: đường cao hạ từ đỉnh A xuống cạnh đối diện

P: nửa chu vi của tam giác p= (a + b + c) : 2

a,b,c là độ dài các cạnh trong tam giác đó.

Ví dụ: Cho tam giác ABC có độ dài 3 cạnh lần lượt là AB = 3 cm, BC = 6 cm, AC= 7cm. Tính đường cao kẻ từ đỉnh A xuống cạnh BC.

Lời giải:

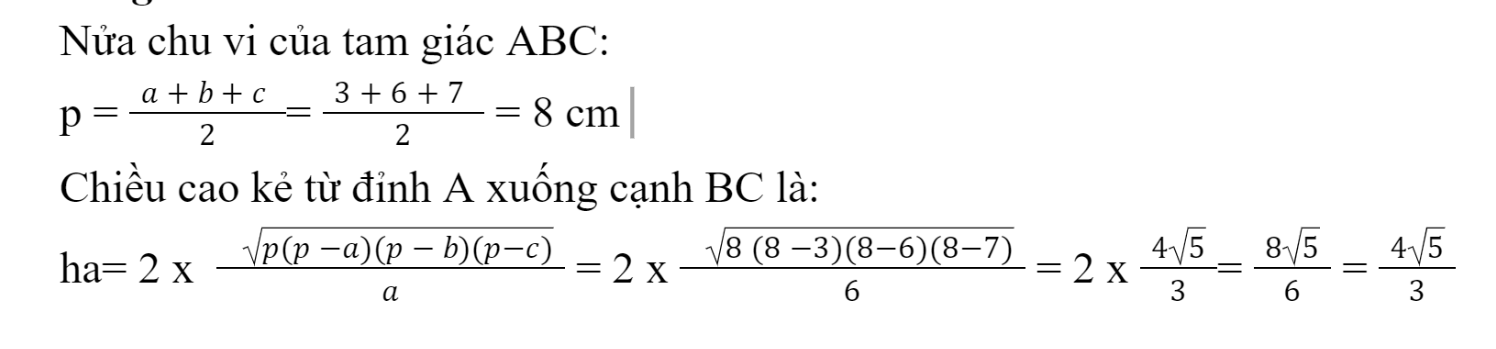
Công thức tính đường cao trong tam giác cân

Giả sử tam giác ABC cân tại A, có AH là đường cao (H BC). Tính đường cao AH ?

Cách tính: Vì tam giác ABC cân tại A nên AH vừa là đường cao, vừa là đường trung tuyến.

Suy ra, H là trung điểm của BC => HB = HC = ½ BC.

Áp dụng định lý Pi-ta-go trong tam giác ABH có:

Ví dụ: Cho tam giác ABC cân tại A có BC = 6  cm,  AB = 5 cm. Tính đường cao AH ( (H BC)

Lời giải:

Tam giác ABC cân tại A có AH là đường cao => AH là đường trung tuyến của tam giác ABC => BH = HC = BC /2 = 6/2 = 3 cm

Áp dụng định lý Pi-ta-go trong tam giác ABH có:

AB^2 = AH^2 + BH^2

=> AH^2 = 5^2 – 3^2 =4^2

=> AH = 4 cm

Công thức tính đường cao trong tam giác đều

Công thức tính đường cao trong tam giác đều là

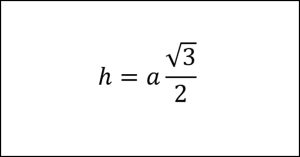
Ví dụ: Cho tam giác ABC đều có độ dài cạnh a = 4. Tính đường cao AH

Lời giải:

Áp dụng công thức :

Vậy đường cao AH =

Công thức tính đường cao trong tam giác vuông

Các công thức tính đường cao trong tam giác vuông như sau:

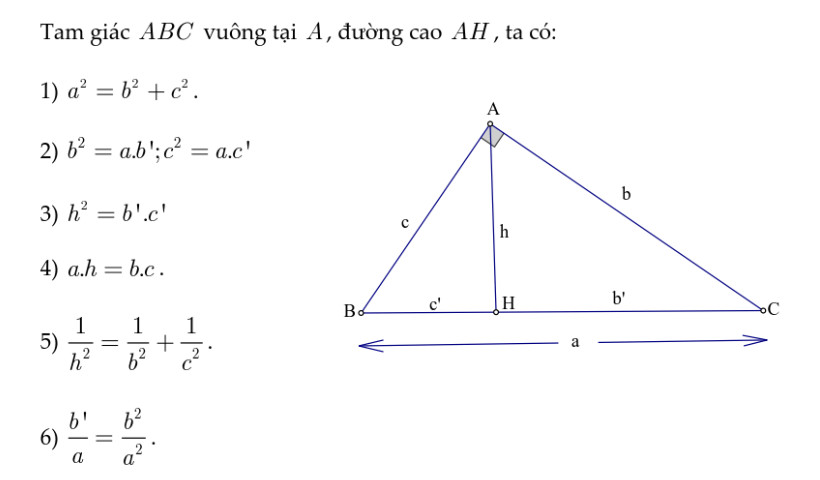
Ví dụ: Cho tam giác ABC vuông tại A, có AH là đường cao (H thuộc BC), AB = 3, AC = 5. Tính đường cao AH

Lời giải.

Hi vọng bài viết trên đây của Công Decor đã cung cấp cho bạn những kiến thức bổ ích về đường cao.  Chúc bạn luôn học tập thật tốt nhé!.

Chu Trang