Nguyên hàm là gì? Bảng nguyên hàm và công thức nguyên hàm?

Nguyên hàm là gì? Bảng nguyên hàm và công thức nguyên hàm? Hãy cùng Công Decor tìm hiểu chi tiết qua bài viết dưới đây nhé!

Lý thuyết về nguyên hàm

Nguyên hàm là gì?

Cho hàm số f(x) xác định trên K, lúc này hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) (với mọi x ∊ K, K có thể là khoảng, đoạn hoặc nửa đoạn trên ℝ).

Kí hiệu nguyên hàm của hàm số f(x) là:

∫f(x)dx=F(x)+C   (∀ C∈R)

Chú ý: Mọi hàm số liên tục trên K đều có nguyên hàm trên K.

3 định lý của nguyên hàm là:

Định lý 1: Giả sử F(x) là một nguyên hàm của f(x) trên K. Khi đó, với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x).

Định lý 2: Trên K, nếu F(x) là một nguyên hàm của hàm số f(x) thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số tùy ý.

Định lý 3: Trên K, tất cả hàm số f(x) liên tục đều có nguyên hàm.

Tính chất của nguyên hàm

– Nếu F(x) có đạo hàm thì:

Tích của nguyên hàm với k là hằng số khác 0:

Tổng, hiệu của nguyên hàm:

Tổng hợp các công thức nguyên hàm

Bảng công thức nguyên hàm cơ bản

Bảng công thức nguyên hàm nâng cao

Bảng công thức nguyên hàm mở rộng

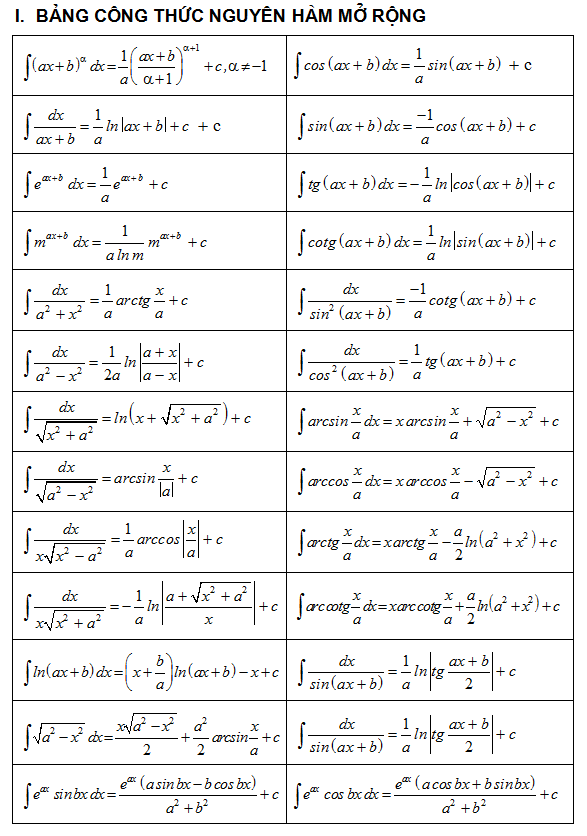
Bảng công thức nguyên hàm lượng giác

Phương pháp giải bài toán nguyên hàm

Phương pháp đổi biến số:

Nếu ∫ f (x) d x = F (x) + C thì ∫f [u(x)]. u’ (x) dx = F [u(x)] + C

Giả sử ta cần tìm họ nguyên hàm I = ∫ f(x) dx, trong đó ta có thể phân tích hàm số đã cho f(x) =  g[u(x) ]. u'(x) thì ta thực hiện phép biến đổi biến đặt t = u(x) ⇒ dt = u'(x) dx. Khi đó, ta thấy I = ∫ g(t) dt = G(t) + C = G [u(x)] + C.

Chú ý: Sau khi ta tìm được họ nguyên hàm theo t thì ta phải thay t = u(x).

Phương pháp tính nguyên hàm, tích phân của hàm số hữu tỷ I = ∫[P(x) / Q(x)]. dx:

Nếu bậc của tử số P(x) ≥ bậc của mẫu số Q(x) → chia đa thức.

Nếu bậc của tử số P(x) ≤ bậc của mẫu số Q(x) → phân tích mẫu Q(x) thành tích số, rồi sử dụng phương pháp chia để đưa về công thức nguyên hàm số.
Nếu mẫu không phân tích được thành tích số→thêm bớt để đổi biến hoặc lượng giác hóa bằng cách đặt X = a tan t, nếu mẫu đưa được về dạng X2 + a2

Nguyên hàm từng phần:

Cho hai hàm số u và v liên tục trên [a;b] và có đạo hàm liên tục trên [a;b]. Khi đó ta có được:

∫ udv = uv – ∫ vdu (*)

Để tính nguyên hàm ∫ udv = uv – ∫ vdu bằng phương pháp từng phần ta làm như sau:

Bước 1: Chọn u, v sao cho f(x) dx = udv (Chú ý: dv = v'(x) dx)

Tính: v = ∫ dv và du =u’dx.

Bước 2: Thay vào công thức (*) và tính ∫ vdu.

Cần phải lựa chọn u và dv hợp lí sao cho ta dễ dàng tìm được v và tích phân ∫ vdu dễ tính hơn ∫ udv.

Mẹo nhớ: “Nhất lô, nhì đa, tam lượng, tứ mũ”

Chu Trang

Tôi là Chu Thị Trang tôi là một nhà sáng tạo nội dung chuyên nghiệp. Tôi có 6 năm làm cộng tác viên cho các tờ báo online nổi tiếng như dân trí, vn express, kênh 14…. Tôi chuyên viết về những vấn đề kinh tế xã hội, đời sống, trang trí nhà cửa.