Cách tính chu vi hình thang? Công thức tính diện tích hình thang?
Cách tính chu vi hình thang? Công thức tính diện tích hình thang?
Hình thang là tứ giác có hai cạnh đối song song với nhau và đây là một hình rất phổ biến. Vậy Công thức tính chu vi và diện tích hình thang là gì? Các bài toán vận dụng như thế nào? Hãy cùng Công Decor tìm hiểu qua bài viết dưới đây nhé!

Chu vi và diện tích hình thang
Hình thang là gì?
Tóm tắt nội dung bài viết
Khái niệm
Hình thang là tứ giác có hai cạnh đối song song với nhau. Hai cạnh này được gọi là hai cạnh đáy của hình thang, hai cạnh còn lại là cạnh bên
Các loại hình thang
Hình thang có các dạng sau:
- Hình thang vuông là hình thang có một góc vuông
- Hình thang cân là hình thang có hai góc kề một cạnh đáy bằng nhau
- Hình bình hành là hình thang có 2 cạnh đáy và 2 cạnh bên song song và bằng nhau
- Hình chữ nhật là hình thang vừa vuông vừa cân
Dấu hiệu nhận biết hình thang
Các dấu hiệu nhận biết hình thang
- Tứ giác có hai cạnh đối song song với nhau
- Hình thang có một góc vuông là hình thang vuông
- Hình thang có hai góc kề một cạnh đáy bằng nhau là hình thang cân
- Hình thang có hai cạnh bên bằng nhau là hình thang cân
- Hình thang có hai đường chéo bằng nhau là hình thang cân
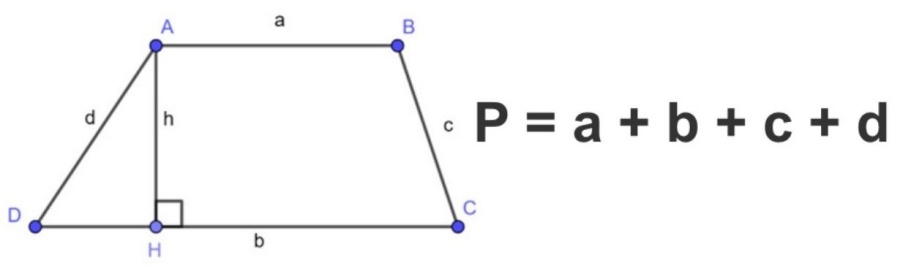
Công thức tính chu vi hình thang
Các tính: Để tính chu vi hình thang, ta lấy tổng của các cạnh bên và cạnh đáy
Chu vi hình thang
Công thức: P = a + b + c + d
Trong đó: P là chu vi của hình thang
a và b là độ dài hai cạnh đáy
c và d là độ dài hai cạnh bên
Ví dụ: Cho hình thang ABCD có độ dài đáy lớn và đáy nhỏ lần lượt là 12 cm và 9 cm. Độ dài cạnh bên là 5 cm và 7 cm. Tính chu vi của hình thang
Lời giải:
Chu vi của hình thang là:
12 + 9 + 5 + 7 = 33 (cm)
Đáp số: 33 cm
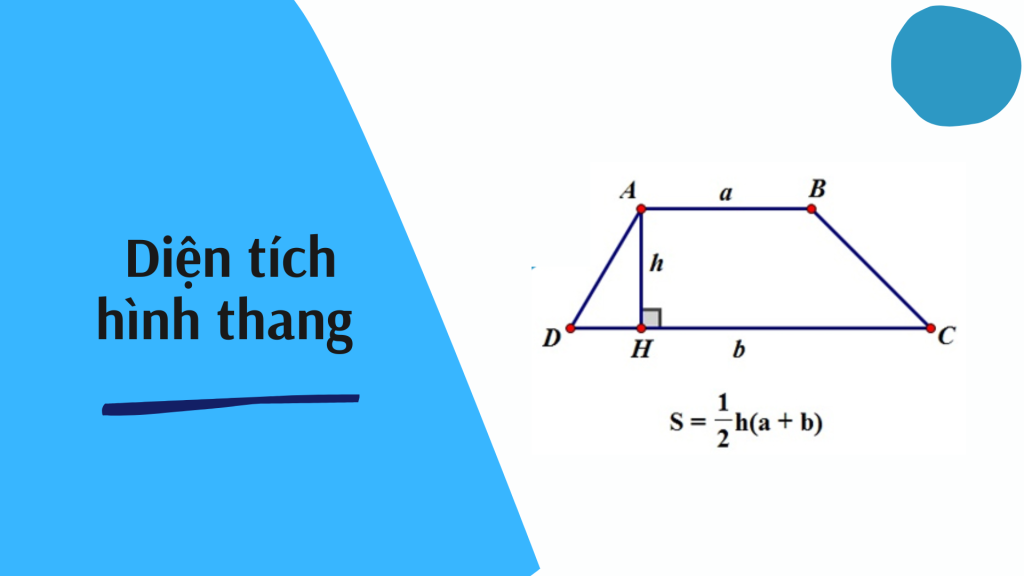
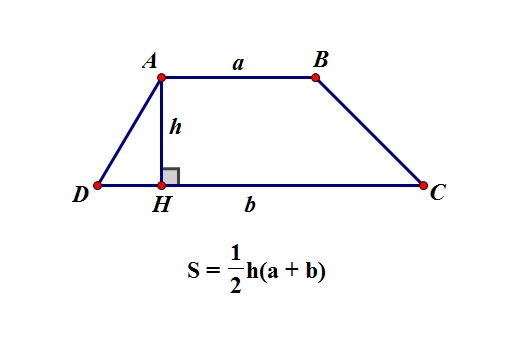
Công thức tính diện tích hình thang
Cách tính: Muốn tính diện tích hình thang, ta lấy đáy lớn cộng với đáy nhỏ rồi nhân với hai
Công thức: S = ( a + b) x h : 2
Diện tích hình thang
Trong đó: S là diện tích hình thang
a và b lần lượt là đáy lớn và đáy nhỏ
h là chiều cao
Bài thơ về diện tích hình thang
Muốn tính diện tích hình thang
Đáy lớn đáy nhỏ ta đem cộng vào
Cộng vào nhân với chiều cao
Chia đôi lấy nửa thế nào cũng ra
Ví dụ: Cho hình thang ABCD có đáy lớn là 15cm, đáy nhỏ là 13 cm, chiều cao là 5 cm. Tính diện tích của hình thang ABCD.
Lời giải:
Diện tích của hình thang ABCD là
(15 + 13 ) x 5 : 2 = 70 (cm2 )
Đáp số: 70 cm2
Bài tập vận dụng
Bài 1: Tính chu vi của hình thang biết đáy lớn đáy nhỏ lần lượt là 8cm và 7cm, hai cạnh bên lần lượt là 3cm và 4 cm.
Lời giải:
Chu vi của hình thang là:
8 + 7 + 3 + 4 = 22 cm
Đáp số: 22 cm
Bài 2: Cho hình thang có hai cạnh bên bằng nhau, chu vi bằng 69 cm, độ dài hai cạnh đáy lần lượt là 15 cm và 18cm. Tính độ dài cạnh bên.
Lời giải:
Tổng độ dài hai cạnh bên của hình thang là
69 – 15 – 18 = 36 cm
Độ dài cạnh bên của hình thang là:
36 : 2 = 18 cm
Đáp số: 18 cm
Bài 3: Tính diện tích hình thang ABCD có đáy lớn và đáy nhỏ lần lượt là 24 cm và 15 cm. Chiều cao của hình thang là 7cm.
Lời giải:
Diện tích của hình thang ABCD là
( 24 + 15 ) x 8 : 2 = 156 cm2
Đáp số: 156 cm2
Bài 4: Hình thang có chiều cao bằng 8cm. Đáy lớn hơn đáy bé 15 cm và đáy bé bằng ⅗ đáy lớn. Tính diện tích của hình thang đó.
Lời giải:
Hiệu số phần bằng nhau là:
5 -2 = 3 (phần)
Độ dài đáy lớn là
15 : 3 x 5 = 25 (cm)
Độ dài đáy bé là:
25 -15 = 10 (cm)
Diện tích của hình thang là:
(25 + 10 ) x 8 : 2 = 140 (cm2 )
Đáp số: 140 cm2
Bài 5: Cho hình thang có tổng độ dài hai đáy là 72 cm gấp 3 lần chiều cao. Tính diện tích của hình thang đó.
Lời giải
Chiều cao của hình thang là:
72 : 3 = 24 cm
Diện tích của hình thang là
72 x 24 : 2 = 864 cm2
Đáp số: 864 cm2
Bài 6: Một thửa ruộng hình thang vuông có cạnh bên vuông góc với 2 đáy có độ dài là 12m, đáy lớn là 35m và đáy nhỏ là 24 m. Tính diện tích của thửa ruộng đó
Lời giải:
Diện tích của thửa ruộng là
(35 + 24 ) x 12 : 2 = 354 m2
Đáp số: 354 m2
Bài viết trên đây là những kiến thức căn bản về công thức tính chu vi và diện tích hình thang và những bài tập vận dụng. Hy vọng rằng những kiến thức mà Công Decor mang lại sẽ giúp ích cho các bạn học sinh trong quá trình học tập và ôn luyện.